Answer: 31%
Explanation:
Formula : Percent of the variability =
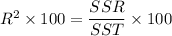
, where
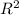 = Coefficient of Determination.
= Coefficient of Determination.
SSR = sum of squares of regression
SST = total sum of squares
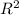 is the proportion of the variation of Y that can be attributed to the variation of x.
is the proportion of the variation of Y that can be attributed to the variation of x.
As per given , we have
SSR = 14.55
SST= 46.8
Then, the percent of the variability in y that can be explained by variability in the regression model =
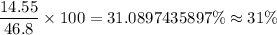
Hence, the percent of the variability in y that can be explained by variability in the regression model = 31%