Question

A pendulum, comprising a light string of length L and a small sphere, swings in the vertical plane. The string hits a peg located a distance d below the point of suspension (Fig. P8.68). (a) Show that if the sphere is released from a height below that of the peg, it will return to this height after the string strikes the peg. (b) Show that if the pendulum is released from rest at the horizontal position (u 5 908) and is to swing in a complete circle centered on the peg, the minimum value of d must be 3L/5.

Answer 1

When a pendulum hits a peg, it will return to its original height if released from below the peg. The minimum value of d, in order for a pendulum to swing in a complete circle centered on a peg, must be 3L/5.

Step-by-step explanation:

A pendulum comprising a light string and a small sphere swings in the vertical plane. When the string hits a peg located below the point of suspension, the sphere will return to its original height if it is released from a height below that of the peg. The reason for this is that when the string hits the peg, the tension in the string abruptly changes direction, causing the sphere to swing back upwards.

If the pendulum is released from rest at the horizontal position and is to swing in a complete circle centered on the peg, the minimum value of d must be 3L/5. This is because when the pendulum is at the lowest point, the tension in the string must be equal to or greater than the weight of the sphere in order to maintain circular motion. The minimum value of d ensures that this condition is satisfied.

Answer 2

the demonstrations are in the description.

Step-by-step explanation:

First of all, reference is made to a picture that may be the one shown attached.

when the string hits the pin, the sphere will continue to swing to the right until a height h'.

a) Initially, the system has only potential energy because it is released with zero velocity from a height h.

if we consider that the system has no energy losses, then all that potential energy must be conserved. Thus, this energy is transformed in principle into kinetic energy and once the kinetic energy is maximum, it will be transformed again into potential energy.

The potential energy is given by:

`E_p = mgh`

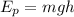
As we can see, potential energy only depends on mass, height and gravity. Since mass and gravity are constant, then for potential energy to be conserved, heights must be the same.

b) the statement probably has a transcription error in question b. Corrected, it would look like:

Show that if the pendulum is released from the horizontal position (∡ = 90) and is to swing in a complete circle centered on the peg, the minimum value of d must be 3L/5.

podemos asumir que la altura cero está dada en el punto de reposo del péndulo, por lo cual la energía inicial (que es potencial) está dada por:

`E_0=MGL`

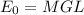
For the pendulum to swing, the tension must always be positive, and as a consequence, the centripetal force must be greater or at least equal to the weight. Mathematically

`mV^2 /(L-d) = mg` (1)

Where:

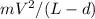`mV^2 /(L-d)` It is the centripetal force that the sphere experiences.

Now, for the sphere to describe the circular motion, the minimum kinetic energy must be:

`(mV^2)/(2) = mgL-2mg(L-d)` (2)

Then, replacing equation 1 in 2:

`(mg(L-d))/(2) = mgL-2mg(L-d)`

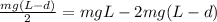
Simplifying:

`L-2L+2d= (L)/(2) - (d)/(2)`

`(5)/(2)d= (3)/(2)L`

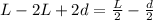
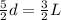
Which means

`d=(3L)/(5)`