Question

Angular and Linear Quantities: A child is riding a merry-go-round that has an instantaneous angular speed of 1.25 rad/s and an angular acceleration of 0.745 rad/s2. The child is standing 4.65 m from the center of the merry-go-round. What is the magnitude of the linear acceleration of the child? Angular and Linear Quantities: A child is riding a merry-go-round that has an instantaneous angular speed of 1.25 rad/s and an angular acceleration of 0.745 rad/s2. The child is standing 4.65 m from the center of the merry-go-round. What is the magnitude of the linear acceleration of the child?

a. 3.46 m/s2

b.4.10 m/s2

c. 8.05 m/s2

d. 7.27 m/s2

e. 2.58 m/s2

Answer 1

To solve this problem we will use the kinematic equations of angular motion in relation to those of linear / tangential motion.

We will proceed to find the centripetal acceleration (From the ratio of the radius and angular velocity to the linear velocity) and the tangential acceleration to finally find the total acceleration of the body.

Our data is given as:

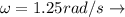`\omega = 1.25 rad/s \rightarrow` The angular speed

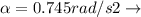`\alpha = 0.745 rad/s2 \rightarrow` The angular acceleration

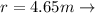`r = 4.65 m \rightarrow` The distance

The relation between the linear velocity and angular velocity is

`v = r\omega`

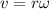
Where,

r = Radius

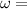`\omega =` Angular velocity

At the same time we have that the centripetal acceleration is

`a_c = (v^2)/(r)`

`a_c = ((r\omega)^2)/(r)`

`a_c = (r^2\omega^2)/(r)`

`a_c = r \omega^2`

`a_c = (4.65 )(1.25 rad/s)^2`

`a_c = 7.265625 m/s^2`

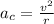
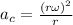
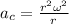
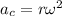
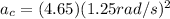
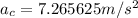
Now the tangential acceleration is given as,

`a_t = \alpha r`

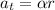
Here,

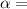`\alpha =` Angular acceleration

r = Radius

`\alpha = (0.745)(4.65)`

`\alpha = 3.46425 m/s^2`

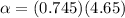
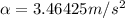
Finally using the properties of the vectors, we will have that the resulting component of the acceleration would be

`|a| = √(a_c^2+a_t^2)`

`|a| = √((7.265625)^2+(3.46425)^2)`

`|a| = 8.049 m/s^2 \approx 8.05 m/s2`

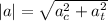
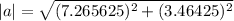
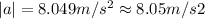
Therefore the correct answer is C.