To solve this problem we will apply the concepts given for the efficiency of an engine which is given as

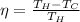
Where
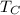 = Temperature of the cold reservoir
= Temperature of the cold reservoir
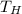 = Temperature of the hot reservoir
= Temperature of the hot reservoir
The efficiency maximum would be given only if
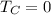
Replacing this value we have
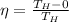
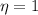
Therefore: Cold reservoir as cold as possible provide the greater efficiency.