Question

Which of the following is an odd function?

f(x) = x3 + 5x2 + x
O F(x)= √x
Of(x) = x2 + x
O f(x) = -x

Answer 1

D

Explanation:

just took test on edge

Answer 2

Option 4

f(x) = -x is an odd function

Solution:

A function is odd if and only if f(–x) = –f(x)

Option 1

`f(x) = x^3 + 5x^2 + x`

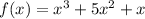
Substitute x = -x in above equation

`f(-x) = (-x)^3 + 5(-x)^2 + (-x)`

Cubes always involve multiplying a number by itself three times, so if the number is negative the cube will always be negative

Ans squaring results in positive

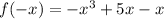`f(-x) = -x^3 + 5x -x` --- eqn 1

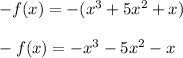`-f(x) = -(x^3 + 5x^2 + x)\\\\-f(x) = -x^3 - 5x^2 - x` ---- eqn 2

Comparing eqn 1 and eqn 2,

`f(-x) \\eq -f(x)`

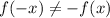
Therefore not an odd function

Option 2

`f(x) = √(x)`

`f(-x) = √(-x)`

`-f(x) = - √(x)`

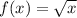
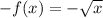
Therefore,

`f(-x) \\eq -f(x)`

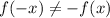
Therefore not an odd function

Option 3

`f(x) = x^2 + x\\\\f(-x) = (-x)^2 + (-x)\\\\f(-x) = x^2 - x`

`-f(x) = -(x^2 + x) = -x^2 - x`

`f(-x) \\eq -f(x)`

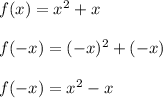
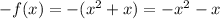
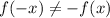
Therefore not an odd function

Option 4

`f(x) = -x\\\\f(-x) = -(-x) = x`

`-f(x) = -(-x) = x`

`f(-x) = -f(x)`

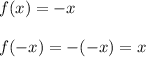
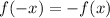
Thus option 4 is correct and it is an odd function