Question

A school district claims that the average teacher in the district earns $45,000 per year. The teacher's union disputes this claim and argues that the average salary is actually less. A random sample of 20 teachers yields a mean salary of $44,500 with a sample standard deviation of $1,750. What's the P­value for a test of the hypothesis that H0 : m = 44,5 00 and Ha : m < 44,500?

a. .01 < P < .02
b. .02 < P < .025
c. .025 < P < .05
d. .05 < P < .10
e. .10 < P < .15

Answer 1

Option e) 0.10 < P < 0.15

Explanation:

We are given the following in the question:

Population mean, μ = $45,000

Sample mean,
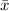`\bar{x}` = $44,500

Sample size, n = 20

Alpha, α = 0.05

Sample standard deviation, s = $1,750

First, we design the null and the alternate hypothesis

`H_(0): m = 44500\\H_A: m < 44500`

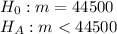
We use one-tailed(left) t test to perform this hypothesis.

Formula:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(s)/(√(n)) }`

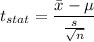
Putting all the values, we have

`t_(stat) = \displaystyle(44500 - 45000)/((1750)/(√(20)) ) = -1.2778`

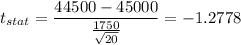
Now, calculating the p-value at degree of freedom 19 and the calculated test statistic,

p-value = 0.108494

Thus,

Option e) 0.10 < P < 0.15