Question

A motorcycle rides on the vertical walls around the perimeter of a large circular room. The friction coefficient between the motorcycle tires and the walls is µ. How does the minimum µ needed to prevent the motorcycle from slipping downwards change with the motorcycle’s speed, s?

a) µ ∝ s0b) µ ∝ s−1/2c) µ ∝ s−1d) µ ∝ s−2e) none of these

Answer 1

option D

Step-by-step explanation:

given,

coefficient of friction between wall and tire = µ

speed of motorcycle = s

friction force = f = μ N

where normal force will be equal to centripetal force

`N = (mv^2)/(r)`

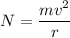
for motorcycle to not to slip weight should equal to the centripetal force

now,

`m g =\mu (mv^2)/(r)`

`\mu =(rg)/(s^2)`

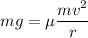
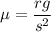
where "rg" is constant

`\mu\ \alpha \ (1)/(s^2)`

`\mu\ \alpha \ s^(-2)`

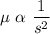
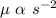
Hence, the correct answer is option D