Answer:
The Range is {3, 6}.
Explanation:
The correct question is
Find the range of the function below if the domain is {-1,0,2} f(x)=x^2 -2x+3
we know that
The domain represents all possible values of x.
The range represents all possible values of f(x)
Substitute all of the possible x-values (domain) into the formula to find all possible f(x) values (the range).
For x=-1
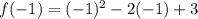
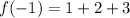
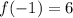
For x=0
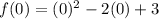
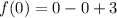
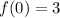
For x=2
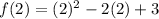
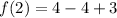
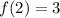
therefore
The Range is {3, 6}.