Question

If a certain cannon is fired from a height of 8.8 meters above the​ ground, at a certain​ angle, the height of the cannonball above the​ ground, h, in​ meters, at​ time, t, in​ seconds, is found by the function h left parenthesis t right parenthesis equals negative 4.9 t squared plus 30.5 t plus 8.8. Find the time it takes for the cannonball to strike the ground.

Answer 1

It would take approximately 6.50 second for the cannonball to strike the ground.

Explanation:

Consider the provided function.

`h(t)=-4.9t^2+30.5t+8.8`

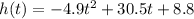
We need to find the time takes for the cannonball to strike the ground.

Substitute h(t) = 0 in above function.

`-4.9t^2+30.5t+8.8=0`

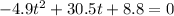
Multiply both sides by 10.

`-49t^2+305t+88=0`

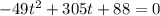
For a quadratic equation of the form
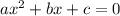`ax^2+bx+c=0` the solutions are:
`x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

Substitute a = -49, b = 305 and c=88

`t=(-305+√(305^2-4\left(-49\right)88))/(2\left(-49\right))=-(-305+√(110273))/(98)\\t = (-305-√(305^2-4\left(-49\right)88))/(2\left(-49\right))= (305+√(110273))/(98)`

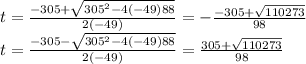
Ignore the negative value of t as time can't be a negative number.

Thus,

`t=(305+√(110273))/(98)\approx6.50`

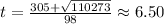
Hence, it would take approximately 6.50 second for the cannonball to strike the ground.