Question

Dave wants to borrow $22,000 from First Finance Bank. The bank

will give him a 15-year loan at an interest rate of 4.85%. How much
Will he pay the bank in interest over the life of the loan? Round to
the nearest hundred dollars.

Answer 1

• Principle=P=22000
• R=4.85%
• T=15yr

Interest be I

`\\ \rm\rightarrowtail I=(PRT)/(100)`

`\\ \rm\rightarrowtail I=(22000(4.85)(15))/(100)`

`\\ \rm\rightarrowtail I=680.41`

Answer 2

$9,000 (to the nearest hundred dollars)

Explanation:

Loans from banks are usually amortizing loans, which is a type of loan that requires regular monthly payments.

To calculate the regular monthly payment:

`\sf PMT=(P\left((r)/(n)\right))/(1-\left(1+(r)/(n)\right)^(-nt))`

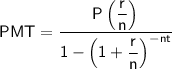
where:

• PMT = regular monthly payment
• P = principal
• r = interest rate in decimal form
• n = number of payments per year
• t = length of loan (in years)

Given:

• P = 22000
• r = 0.0485
• n = 12
• t = 15

`\sf PMT=(2000\left((0.0485)/(12)\right))/(1-\left(1+(0.0485)/(12)\right)^(-12 \cdot 15))=172.2604115...`

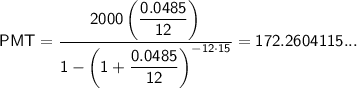
Number of months in 15 years = 15 × 12 = 180

⇒ Total payment over the term of the loan = 180 × 172.2604115...

= 31006.87406...

Total interest = total payment - principal

= 31006.87406... - 22000

= 9006.87406...

= $9,000 (to the nearest hundred dollars)