Answer:
a)
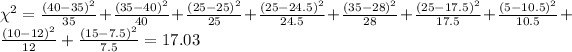

And we can find the p value using the following excel code:
"=1-CHISQ.DIST(17.03,4,TRUE)"
Since the p value is lower than the significance level we can reject the null hypothesis at 5% of significance, and we can conclude that we have association or dependence between the two variables.
b)
P(E|Ex)= P(EΛEx )/ P(Ex) = (40/215)/ (70/215)= 40/70=0.5714
P(E|Gx)= P(EΛGx )/ P(Gx) = (35/215)/ (80/215)= 35/80=0.4375
P(E|Fx)= P(EΛFx )/ P(Fx) = (25/215)/ (50/215)= 25/50=0.5
P(G|Ex)= P(GΛEx )/ P(Ex) = (25/215)/ (70/215)= 25/70=0.357
P(G|Gx)= P(GΛGx )/ P(Gx) = (35/215)/ (80/215)= 35/80=0.4375
P(G|Fx)= P(GΛFx )/ P(Fx) = (10/215)/ (50/215)= 10/50=0.2
P(F|Ex)= P(FΛEx )/ P(Ex) = (5/215)/ (70/215)= 5/70=0.0714
P(F|Gx)= P(FΛGx )/ P(Gx) = (10/215)/ (80/215)= 10/80=0.125
P(F|Fx)= P(FΛFx )/ P(Fx) = (15/215)/ (50/215)= 15/50=0.3
And that's what we see here almost all the conditional probabilities are higher than 0.2 so then the conclusion of dependence between the two variables makes sense.
Explanation:
A chi-square goodness of fit test "determines if a sample data matches a population".
A chi-square test for independence "compares two variables in a contingency table to see if they are related. In a more general sense, it tests to see whether distributions of categorical variables differ from each another".
Assume the following dataset:
Quality management Excellent Good Fair Total
Excellent 40 35 25 100
Good 25 35 10 70
Fair 5 10 15 30
Total 70 80 50 200
Part a
We need to conduct a chi square test in order to check the following hypothesis:
H0: There is independence between the two categorical variables
H1: There is association between the two categorical variables
The level of significance assumed for this case is

The statistic to check the hypothesis is given by:
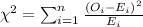
The table given represent the observed values, we just need to calculate the expected values with the following formula
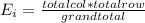
And the calculations are given by:
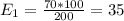

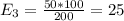
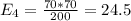
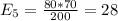
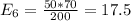
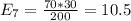
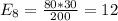
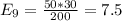
And the expected values are given by:
Quality management Excellent Good Fair Total
Excellent 35 40 25 100
Good 24.5 28 17.5 85
Fair 10.5 12 7.5 30
Total 70 80 65 215
And now we can calculate the statistic:
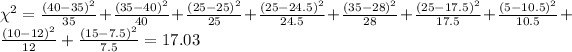
Now we can calculate the degrees of freedom for the statistic given by:

And we can calculate the p value given by:

And we can find the p value using the following excel code:
"=1-CHISQ.DIST(17.03,4,TRUE)"
Since the p value is lower than the significance level we can reject the null hypothesis at 5% of significance, and we can conclude that we have association or dependence between the two variables.
Part b
We can find the probabilities that Quality of Management and the Reputation of the Company would be the same like this:
Let's define some notation first.
E= Quality Management excellent Ex=Reputation of company excellent
G= Quality Management good Gx=Reputation of company good
F= Quality Management fait Ex=Reputation of company fair
P(EΛ Ex) =40/215=0.186
P(GΛ Gx) =35/215=0.163
P(FΛ Fx) =15/215=0.0697
If we have dependence then the conditional probabilities would be higher values.
P(E|Ex)= P(EΛEx )/ P(Ex) = (40/215)/ (70/215)= 40/70=0.5714
P(E|Gx)= P(EΛGx )/ P(Gx) = (35/215)/ (80/215)= 35/80=0.4375
P(E|Fx)= P(EΛFx )/ P(Fx) = (25/215)/ (50/215)= 25/50=0.5
P(G|Ex)= P(GΛEx )/ P(Ex) = (25/215)/ (70/215)= 25/70=0.357
P(G|Gx)= P(GΛGx )/ P(Gx) = (35/215)/ (80/215)= 35/80=0.4375
P(G|Fx)= P(GΛFx )/ P(Fx) = (10/215)/ (50/215)= 10/50=0.2
P(F|Ex)= P(FΛEx )/ P(Ex) = (5/215)/ (70/215)= 5/70=0.0714
P(F|Gx)= P(FΛGx )/ P(Gx) = (10/215)/ (80/215)= 10/80=0.125
P(F|Fx)= P(FΛFx )/ P(Fx) = (15/215)/ (50/215)= 15/50=0.3
And that's what we see here almost all the conditional probabilities are higher than 0.2 so then the conclusion of dependence between the two variables makes sense.