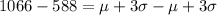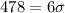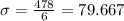Question

Suppose that the distribution is bell-shaped. If approximately 99.7% of the lifetimes lie between 568 hours and 1066 hours, then the approximate value of the standard deviation for the distribution, according to the empirical rule, is .

Answer 1

`\sigma =(478)/(6)=79.667`

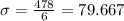
Explanation:

The empirical rule, also referred to as "the three-sigma rule or 68-95-99.7 rule, is a statistical rule which states that for a normal distribution, almost all data falls within three standard deviations (denoted by σ) of the mean (denoted by µ)". The empirical rule shows that 68% falls within the first standard deviation (µ ± σ), 95% within the first two standard deviations (µ ± 2σ), and 99.7% within the first three standard deviations (µ ± 3σ).

And on this case since we are within 3 deviations (because we have 99.7% of the data between 568 and 1066hours), the result obtained using the z score agrees with the empirical rule.

So on this case we can find the standard deviation on this ways:

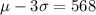`\mu -3\sigma = 568` (1)

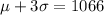`\mu +3\sigma = 1066` (2)

If we subtract conditions (2) and (1) we got:

`1066-588 =\mu +3\sigma -\mu +3\sigma`

`478= 6\sigma`

`\sigma =(478)/(6)=79.667`