Question

The radius of a sphere increases at a constant rate of 2 com/min at the time when the volume of the sphere is 40 cm^3ç What is the rate of increase of the volume in cm^3/min?

Answer 1

`(dV)/(dt)=525 cm^(3)/min`

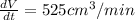
Explanation:

The volume of a sphere is:

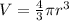`V=(4)/(3)\pi r^(3)` (1)

We know that:

• dr/dt = 2 cm/min (increasing rate of radius)
• V = 40 cm³

If we take the derivative of (1) with respect of time t, we ca n find the rate of increase of the volume.

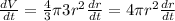`(dV)/(dt)=(4)/(3)\pi 3r^(2)(dr)/(dt)=4\pi r^(2)(dr)/(dt)` (2)

We also know that the volume is 40 cm³, then using the (1) we can get the radius at this value.

Solving (1) for r, we have:

`r=\left((3\cdot V)/(4\pi)\right)^(1/3)=\left((3\cdot 400)/(4\pi)\right)^(1/3)=4.57 cm`

Finally dV/dt will be:

`(dV)/(dt)=4\pi (4.57)^(2)\cdot 2=525 cm^(3)/min`

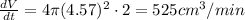
I hope it helps you!