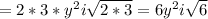Question

Simplify the radicals.
Someone please help because my book doesnt explain how to do this.​

Answer 1

Answer:
`6y^2i√(6)`

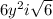
Explanation:

For this exercise it is important to remember the following property:

`\sqrt[n]{a^n}=a^{({(n)/(n))}}=a`

Then, given the expression:

`√(-216y^4)`

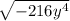
You can follow these steps in order to simplify it:

1. Descompose 216 into its prime factors:

`216=2*2*2*3*3*3`

2. The Product of powers property states that:

`(a^m)(a^n)=a^((m+n))`

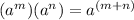
Then:

`216=2^2*2*3^2*3`

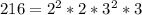
3. Now you can substitute:

`=√(-2^2*2*3^2*3*y^4)`

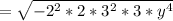
4. Finally, substituting
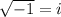`√(-1)=i` and simplifying, you get:

`=2*3*y^2i√(2*3)=6y^2i√(6)`