Problem 1
The domain is
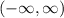 which is the same as saying
which is the same as saying
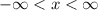 to indicate "the set of all real numbers". This is because the graph stretches on forever in both left/right directions due to the arrows at each endpoint.
to indicate "the set of all real numbers". This is because the graph stretches on forever in both left/right directions due to the arrows at each endpoint.
Answer:
Domain =
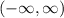
============================================================
Problem 2
The range is
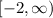 which is the same as writing
which is the same as writing
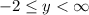 aka
aka
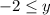 aka
aka
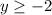 .
.
The lowest y can go is y = -2 as shown by the vertex point. We can have y = -2 or larger. Note the square bracket next to the -2 in
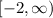 which means we include -2 as part of the interval.
which means we include -2 as part of the interval.
Answers:
Range =
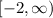
============================================================
Problem 3
This time we don't have arrows at the endpoints. Rather, we have filled in circles or closed endpoints.
The smallest x can be is x = -5 as shown by the left-most endpoint.
The largest x can get is x = 5 as shown by the right-most endpoint.
The allowed interval for all possible x inputs is
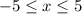 which condenses into the interval notation [-5, 5]. Use square brackets to include each endpoint.
which condenses into the interval notation [-5, 5]. Use square brackets to include each endpoint.
Answer:
Domain = [-5, 5]
============================================================
Problem 4
The range is the set of y values spanning from the lowest/smallest y value of y = -3 to the largest y = 3, which leads to
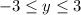 and further to [-3, 3]. We include both endpoints.
and further to [-3, 3]. We include both endpoints.
Answer:
Range = [-3, 3]