Question

The greatest common divisor of two positive integers less than $100$ is equal to $3$. Their least common multiple is twelve times one of the integers. What is the largest possible sum of the two integers?

Answer 1

129

Explanation:

Let a and b be two numbers.

We have been given that the greatest common divisor of two positive integers less than 100 is equal to 3. We can represent this information as
`GCD(a,b)=3`.

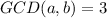Their least common multiple is twelve times one of the integers. We can represent this information as
`LCM(a,b)=12a`.

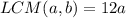Now, we will use property
`GCD(x,y)*LCM(x,y)=xy`.

Upon substituting our given values, we will get:

`3*12a=ab`

`36a=ab`

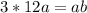
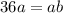
Switch sides:

`ab=36a`

`(ab)/(a)=(36a)/(a)`

`b=36`

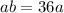
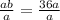
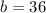
Now, we need to find a number less than 100, which is co-prime with 12 after dividing by 3.

The greatest multiple of 3 less than 100 is 99, but it is not co-prime with 12 after dividing by 3.

Similarly 96 is also not co-prime with 12 after dividing by 3.

We know that greatest multiple of 3 (less than 100), which is co-prime with 12, is 93.

Let us add 36 and 93 to find the largest possible sum of the required two integers as:

`36+93=129`

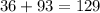
Therefore, the required largest possible sum of the two integers is 129.