Question

A computer can sort x objects in t seconds, as modeled by the functio

below:
1=0.005x2 + 0.002.x
How many objects are required to keep the computer busy for exactly
seconds?
Round to the nearest whole object.

Answer 1

Question:

A computer can sort x objects in t seconds, as modeled by the function below:

t=0.005x^2+0.002x

How many objects are required to keep the computer busy for exactly 9 seconds?

Round to the nearest whole object.

Answer:

42 objects are required to keep the computer busy for exactly 9 seconds

Solution:

Given function is:

Computer can sort x objects in t seconds, as modeled by the function below:

`t = 0.005x^2+0.002x`

We have to find number of objects required to keep the computer busy for exactly 9 seconds

Therefore t = 9

Substitute t = 9 in given function

`9 = 0.005x^2+0.002x\\\\0.005x^2+0.002x - 9 = 0`

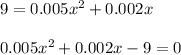
Let us solve the above equation by quadratic formula,

`\text {For a quadratic equation } a x^(2)+b x+c=0, \text { where } a \\eq 0\\\\x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

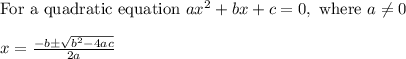
Using the above formula,

`\text{ for } 0.005x^2+0.002x - 9 = 0 , \text{ we have } a = 0.005 ; b = 0.002 ; c = -9`

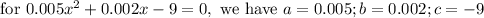
Substituting the values of a = 0.005 ; b = 0.002 ; c = -9 in above quadratic formula we get,

`\begin{aligned}&x=(-0.002 \pm √(0.180004))/(0.01)\\\\&x=(-0.002 \pm 0.4242)/(0.01)\\\\&x=(-0.002+0.4242)/(0.01) \text { or } x=(-0.002-0.4242)/(0.01)\\\\&x=42.22 \text { or } x=-42.62\end{aligned}`

Ignoring negative value,

x = 42.22 ≈ 42

Thus 42 objects are required to keep the computer busy for exactly 9 seconds