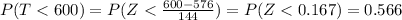Answer:
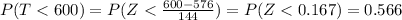
Explanation:
Previous concepts
The central limit theorem states that "if we have a population with mean μ and standard deviation σ and take sufficiently large random samples from the population with replacement, then the distribution of the sample means will be approximately normally distributed. This will hold true regardless of whether the source population is normal or skewed, provided the sample size is sufficiently large".
The exponential distribution is "the probability distribution of the time between events in a Poisson process (a process in which events occur continuously and independently at a constant average rate). It is a particular case of the gamma distribution". The probability density function is given by:
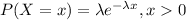
And 0 for other case. Let X the random variable that represent "The number of years a radio functions" and we know that the distribution is given by:
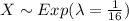
Or equivalently:
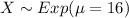
Solution to the problem
For this case we are interested in the total T, and we can find the mean and deviation for this like this:
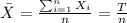
If we solve for T we got:
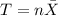
And the expected value is given by:
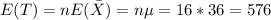
And we can find the variance like this:

And then the deviation is given by:
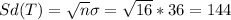
And the distribution for the total is:
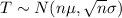
And we want to find this probability:
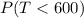
And we can use the z score formula given by:
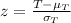
And replacing we got this: