
Given :-
- Quadrilateral PLAY is a kite.
- The length of PA = 12 cm and LY = 6 cm
Part 1 :-
- The area of Quadrilateral PLAY is 36 cm²
Part 2 :-
Here, we have,
- The length PA = 12 cm and LY = 6 cm
- Here, PA and LY are the diagonal of quadrilateral PLAY
We know that,
Area of kite
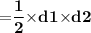
Subsitute the required values,
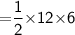
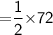

Hence, The area of quadrilateral PLAY is 36 cm²
Part 3 :-
Pythagoras theorem justifies our answers because the diagonals of rhombus are bisects each other at 90°
According to this theorem
- The sum of squares of the base and perpendicular height of the triangle are equal to the square of hypotenuse.
That is ,
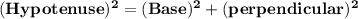
By using this theorem in Quadrilateral PLAY
- We can find the length of diagonals of kite and it's area.
[ Note :- Please refer the attachment for the correct diagram ]