Question

Find the domain of -1/x^2-4

Answer 1

`\mathbb{R}-\{0\}`

`(-\infty,0)\ U\ (0,+\infty)`

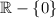
Explanation:

The domain of a Function

Given a real function f(x), the domain of f is made of all the values x can take, such that f exists. The function given in the question is

`\displaystyle f(x)=-(1)/(x^2)-4`

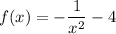
Finding the domain of a function is not possible by giving x every possible value and check if f exists in all of them. It's better to find the values where f does NOT exist and exclude those values from the real numbers.

Since f is a rational function, we know the denominator cannot be 0 because the division by 0 is not defined, so we use the denominator to find the values of x to exclude from the domain.

We set

`x^2=0`

Or equivalently

x=0

The domain of f can be written as

`\mathbb{R}-\{0\}`

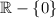
Or also

`(-\infty,0)\ U\ (0,+\infty)`