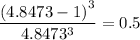Question

A boy thinks he has discovered a way to drink extra orange juice without alerting his parents. For every cup of orange juice he takes from a container of orange juice, he pours one cup of water back into the container. If he completes this process three times on the same container of juice, the resulting mixture will be exactly 50% water and 50% juice. How many cups of orange juice were originally in the container. (P.S ITS NOT 6)​

Answer 1

x=4.8473 cups

Explanation:

Concentration of Liquids

It measures the amount of substance present in a mixture, often expressed as %. If there is an volume x of a substance in a total volume mix of y, the concentration is given by

`\displaystyle C=(x)/(y)`

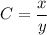
It we take a sample of that mixture, we must consider that we are getting only the substance, but all the mixture (assumed it has been uniformly mixed). For example, if we take a glass of liquid from a 80% mixture of juice, the glass will also have a 80% of juice.

Let's solve the problem sequentially. At first, let's assume all the container is full of x cups of juice. Its concentration is 100%. Now let's take 1 cup of pure juice and replace it by 1 cup of pure water. The new amount of juice in the container is

x-1 cups of juice.

The new concentration is

`\displaystyle (x-1)/(x)`

The boy takes a second cup of liquid, but this time it's not pure juice, it has a mixture of juice and water with a concentration computed above. Now the amount of juice is

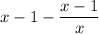`\displaystyle x-1-(x-1)/(x)` cups of juice.

Simplifying, the cups of juice are

`\displaystyle (\left (x-1\right)^2)/(x)`

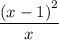
The new concentration is

`\displaystyle (\left (x-1\right)^2)/(x^2)`

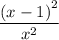
For the third time, we now have

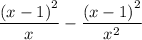`\displaystyle (\left (x-1\right)^2)/(x)-(\left (x-1\right)^2)/(x^2)` cups of juice.

Simplifying, the final amount of juice is

`\displaystyle (\left (x-1\right)^3)/(x^2)`

And the final concentration is

`\displaystyle (\left (x-1\right)^3)/(x^3)`

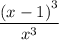
According to the conditions of the question, this must be equal to 50% (0.5)

`\displaystyle (\left (x-1\right)^3)/(x^3)=0.5`

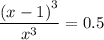
Taking cubic roots

`\displaystyle \sqrt[3]{(\left (x-1\right)^3)/(x^3)}=\sqrt[3]{0.5}`

`\displaystyle (\left (x-1\right))/(x)=\sqrt[3]{0.5}`

Operating and joining like terms

`\displaystyle x-\sqrt[3]{0.5}\ x=1`

Solving for x

`\displaystyle x=\frac{1}{1-\sqrt[3]{0.5}}`

`x=4.8473\ cups`

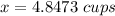
Let's test our result

Final concentration:

`\displaystyle (\left (4.8473-1\right)^3)/(4.8473^3)=0.5`