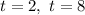Question

Please help me and show steps! I would really appreciate it!

Answer 1

The aircraft has a height of 1000 m at t=2 sec, and at t=8 sec

Explanation:

Finding Exact Roots Of Polynomials

A polynomial can be expressed in the general form

`\displaystyle p(x)=a_nx^n+a_(n-1)\ x^(n-1)+...+a_1\ x+a_0}`

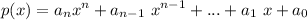
The roots of the polynomial are the values of x for which

`P(x)=0`

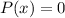
Finding the roots is not an easy task and trying to find a general solution has been discussed for centuries. One of the best possible approaches is trying to factor the polynomial. It requires a good eye and experience, but it gives excellent results.

The function for the trajectory of an aircraft is given by

`\displaystyle h(x)=0.5(-t^4+10t^3-216t^2+2000t-1200)`

We need to find the values of t that make H=1000, that is

`\displaystyle 0.5(-t^4+10t^3-216t^2+2000t-1200)=1000`

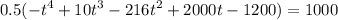
Dividing by -0.5

`\displaystyle t^4-10t^3+216t^2-2000t+1200=-2000`

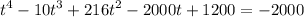
Rearranging, we set up the equation to solve

`\displaystyle t^4-10t^3+216t^2-2000t+3200=0`

Expanding some terms

`\displaystyle t^4-8t^3-2t^3+200t^2+16t^2-1600t-400t+3200=0`

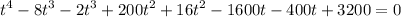
Rearranging

`\displaystyle t^4-8t^3+200t^2-1600t-2t^3+16t^2-400t+3200=0`

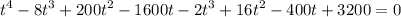
Factoring

`\displaystyle t(t^3-8t^2+200t-1600)-2(t^3-8t^2+200t-1600)=0`

`\displaystyle (t-2)(t^3-8t^2+200t-1600)=0`

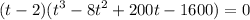
This produces our first root t=2. Now let's factor the remaining polynomial

`\displaystyle t^2(t-8)+200(t-8)=0`

`\displaystyle (t^2+200)(t-8)=0`

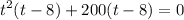
This gives us the second real root t=8. The other two roots are not real numbers, so we only keep two solutions

`\displaystyle t=2,\ t=8`