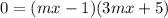Question

`3m ^(2) x ^(2) + 2mx - 5 = 0`

Answer?
With detailed steps please. Thank you! ​

Answer 1

We could factor the usual way but let's try Dr. Po Shen Loh's "new" method.

`3m^2x^2 + 2mx - 5 = 0`

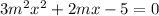
First step is to rewrite as a monic,

`x^2 + (2m)/(3m^2) x - (5)/(3m^2) = 0`

`x^2 + (2)/(3m) x - (5)/(3m^2) = 0`

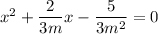
Now we need two numbers which add to 2/3m and multiply to -5/3m². If they add to 2/3m they average to 1/3m so they're 1/3m-u and 1/3m+u for some u. The product of those two is -5/3m² so we write:

`\left( (1)/(3m)-u \right)\left( (1)/(3m) +u \right) = -(5)/(3m^2)`

`(1)/(9m^2)-u^2 = -(5)/(3m^2)`

`u^2 = (1)/(9m^2) +(5(3))/((3)3m^2) = (16)/(9m^2)`

`u = \pm (4)/(3m)`

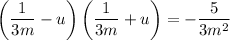
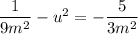
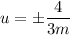
So our equation

`0=x^2 + (2m)/(3m^2) x - (5)/(3m^2)`

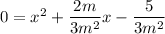
factors as

`0= \left( x +(1)/(3m)-(4)/(3m)\right) \left( x + (1)/(3m) + (4)/(3m)\right)`

`0= \left(x - (1)/(m)\right) \left(x +(5)/(3m) \right)`

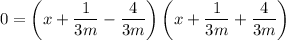
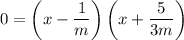
so has roots

`x= (1)/(m) \textrm{ or } x = -(5)/(3m)`

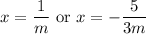
The more standard factorization with the same result is

`0=(mx-1)(3mx+5)`