Question

O find the minimum value of the quadratic expression −4x2+8x−25,

−
4
x
2
+
8
x
−
25
,
Marla used the following steps to complete the square:

Step 1: −4(x2+8x)−25
−
4
(
x
2
+
8
x
)
−
25

Step 2: −4(x2+8x+16−16)−25
−
4
(
x
2
+
8
x
+
16
−
16
)
−
25

Step 3: −4(x2+8x+16)+64−25
−
4
(
x
2
+
8
x
+
16
)
+
64
−
25

Step 4: −4(x+4)2+39
−
4
(
x
+
4
)
2
+
39

Did Marla use the correct steps to complete the square?

Answer 1

Marla didn't use the right steps to complete the square. Maria made a mistake in step 1, she put 8x instead of -2x

Explanation:

we have

`-4x^(2)+8x-25`

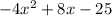
This is a vertical parabola open downward

The vertex is a maximum

Find the vertex

step 1

Factor the leading coefficient -4

`-4(x^(2)-2x)-25`

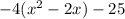
step 2

Complete the square

`-4(x^(2)-2x+1-1)-25`

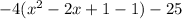
step 3

`-4(x^(2)-2x+1)-25+4`

`-4(x^(2)-2x+1)-21`

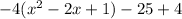
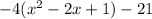
step 4

Rewrite as perfect squares

`-4(x-1)^(2)-21`

the vertex is the point (1,-21)

so

The maximum value of the quadratic equation is (1,-21)

therefore

Marla didn't use the right steps to complete the square. Maria made a mistake in step 1, she put 8x instead of -2x