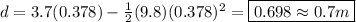Hi there!
Begin by solving for the time it takes the frog to reach the top of its trajectory. (Vertical velocity = 0 m/s)
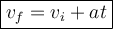
vf = final velocity (0 m/s)
vi = initial velocity (3.7 m/s)
a = acceleration due to gravity (9.8 m/s²)
t = time (s)
Plug in the known values:
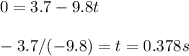
Now, we can use the following kinematic equation:
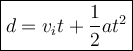
d = displacement (m)
vi = initial velocity (3.7 m/s)
a = acceleration (9.8 m/s²)
t = time (0.378 sec)
Plug in the given values: