Question

Given: △ABC, m∠A=60°,
m∠C=45°, AB=9
Find: Perimeter of △ABC,
Area of △ABC

Answer 1

Perimeter of ΔABC:
`(27)/(2)` +
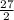`(9)/(2) * \sqrt6` units

Area of ΔABC:
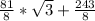`(81)/(8)*\sqrt3 + (243)/(8)` units

Skills required: HS Geo, Special Triangles

Explanation:

1) The best option is to break down this triangle. Let's draw an altitude from Point B down to Segment AC. The point from the altitude that intersects AC is Point D. BD is the height of our triangle, AC is the base.

2) Angle A is 60 degrees, and since Angle BDA is 90 degrees, Angle ABD is 30 degrees. We can use the 30-60-90 degree right triangle property for the triangle BDA.

• This states that if the side opposite the 30 degree angle is
  `x`, the side opposite the 60 degree angle is
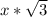  `x*\sqrt3`, and the side opposite the 90 degree angle is
  `2x`.

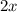AB is 9 units, and it is opposite the 90 degree angle. This means that
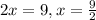`2x=9, x = (9)/(2)` ==> This then means that AD, the segment opposite the 30 degree angle in this triangle is
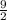`(9)/(2)` units. Segment BD (the height) is
`(9)/(2) * \sqrt3`.

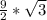3) Angle C is 45 degrees, and Angle BDC is 90 degrees, which means that Angle CBD is 45 degrees. We can use the 45-45-90 degree right triangle property for the triangle BCD.

• This states that if the side opposite the 45 degree angle is
  `x`, the other side opposite a 45 degree angle is also
  `x`, but the hypotenuse (side opposite the right (90 degree) angle) is
  `√(2)*x`.

BD is
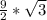`(9)/(2) * \sqrt3`, which means DC is the same. BC, which is the hypotenuse is BD multiplied by square-root-2, which is
`(9)/(2) * \sqrt6`.

4) Area is
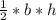`(1)/(2)*b*h`, the base (b) is AC (which is
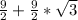`(9)/(2)+(9)/(2)*\sqrt3`), the height is BD (
`(9)/(2)*\sqrt3`). When multiple you will get
`(81)/(4)*\sqrt3 + (243)/(4)`, then this multiplied by 1/2 is

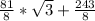`(81)/(8)*\sqrt3 + (243)/(8)` <--> this is the area!

5) Perimeter is just the sum of all side: 9 +
`(9)/(2)` +
`(9)/(2) * \sqrt6` =
`(27)/(2)` +
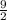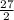`(9)/(2) * \sqrt6` unit