Answer:
Shift "h" units to the right, "k" units up, and reflect over the x or y axis when needed.
Explanation:
1) I want to talk about reflections first.
- Reflections across the x-axis -->
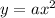 , a is the coefficient. if a is negative, then the equation should be reflected across the x-axis. This is known as a vertical reflection.
, a is the coefficient. if a is negative, then the equation should be reflected across the x-axis. This is known as a vertical reflection. - Reflections across the y-axis -->
 , b is the coefficient. If b is negative, then reflect the equation over the y-axis. There are cases where the reflection across the y-axis does not change anything. But, let's say its
, b is the coefficient. If b is negative, then reflect the equation over the y-axis. There are cases where the reflection across the y-axis does not change anything. But, let's say its
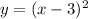 ... the reflection across the y-axis is different (that equation is:
... the reflection across the y-axis is different (that equation is:
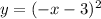 )
)
2) Rigid transformations
- Horizontal transformations (to the left or right):
 , factor out b from "bx-h" and whatever h equals is the units to the right. If h is a negative number, then you move to the left.
, factor out b from "bx-h" and whatever h equals is the units to the right. If h is a negative number, then you move to the left. - Vertical transformations (up and down):
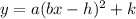 ... k is just the units up... if k is negative then we move it down.
... k is just the units up... if k is negative then we move it down.
Example (check image for visual)
We transform
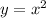 to
to
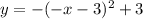 , you move right 3, then reflect across the x-axis, then reflect across y-axis, then move 3 up.
, you move right 3, then reflect across the x-axis, then reflect across y-axis, then move 3 up.
--------------------------------------------------------------------------------------------------------------
Note: In the image, the red line is the original function, the blue one is the transformed function. See if you can follow along with the verbal instructions I gave above.