Question

Find sum of arithmetic series where a1 = 7, n=31, nth a =127

Answer 1

Sum of arithmetic series is
`2077`

Explanation:

We have
`n`th term of arithmetic sequence

`a+(n-1)d`

Here

`a+(n-1)d=127\\\\7+(31-1)d=127\\\\d=(120)/(30) \\\\=4`

Sum of arithmetic sequence
`=(n)/(2) (2a+(n-1)d)`

`=(31)/(2) (2*7+(31-1)4)\\\\=(31)/(2) (14+120)\\\\=31*67\\\\=2077`

Answer 2

The sum of arithmetic series is 2077.

Step-by-step explanation:

Solution :

Here we have provided that :

• »»
  `\rm{a_1}` = 1
• »»
  `\rm{n}` = 31
• »»
  `\rm{a_n}` = 127

We need to find :

• »» The sum of arithmetic series.

Here's the required formula to find the sum of arithmetic series :

`\longrightarrow{\pmb{\sf S = (n)/(2) \Big(a_1 + a_n \Big)}}`

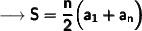
Substituting all the given values in the formula to find the sum of arithmetic series :

`{\longrightarrow{\sf S = (n)/(2) \Big(a_1 + a_n \Big)}}`

`{\longrightarrow{\sf S = (31)/(2) \Big(7 + 127 \Big)}}`

`{\longrightarrow{\sf S = (31)/(2) \Big(134 \Big)}}`

`{\longrightarrow{\sf S = (31)/(2) * 134 }}`

`{\longrightarrow{\sf S = \frac{31}{\cancel{2}} * \cancel{134 }}}`

`{\longrightarrow{\sf S = 31 * 67}}`

`{\longrightarrow{\sf S = 2077}}`

`\star \: {\underline{\boxed{\sf{\red{S = 2077}}}}}`

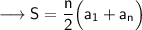
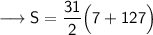
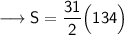
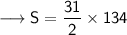
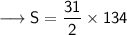
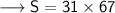
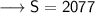
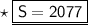
Hence, the sum of arithmetic series is 2077.

`\rule{300}{1.5}`