Question

Solve similar triangles (advanced)

Answer 1

Answer: 18/7

This approximates to 2.5714

=====================================================

Step-by-step explanation:

The two triangles are similar. We can use the AA (angle angle) theorem to prove this claim.

Because
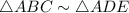`\triangle ABC \sim \triangle ADE`, this means:

• side AB corresponds to side AD. The letters from AB are the first two letters of ABC while AD are the first two letters from ADE.
• side BC corresponds to DE. We have BC as the last two letters of ABC and DE the last two letters of ADE

As those bullet points above mention, the order of ABC and ADE matters to allow us to pair up the corresponding angles and corresponding sides.

From that, we can form the proportion below to solve for x

AB/AD = BC/DE

3/(3+4) = x/6

3/7 = x/6

3*6 = 7*x

18 = 7x

7x = 18

x = 18/7

You could convert this to the approximate decimal form 18/7 = 2.5714, but I think it's better to keep it as a fraction.