Question

How do you solve : 3x^4 - 11x^3 -x^2 + 19x + 6

You can't use long division in this equation.

Answer 1

Explanation:

This is a polynomial so we can use rational roots Theorem to solve the equation.

The rational roots simply states that the roots of a polynomial, in the form of

`p{x}^(n) + ax {}^(n - 1) + bx {}^(n - 2) .....r {}^(0)`

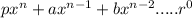
The possible roots of the polynomial are the factors of

p/r.

We say r^0 to represent the constant and p to represent the leading coeffceint.

So the rational roots states the possible roots of a polynomial is

the factors of leading coeffceint/ the factors of the constant.

In this case, the polynomial leading coeffecient is 3 and its constant is 6 so we do the factors of 3 divided by the factors of 6.

The factors of 3, are plus or minus 1 and 3. divided by factors of 6 which are plus or minus 1,2,3,6. So our possible roots are

positive or negative (1,1/2, 1/3,1/6, 3, 3/2).

Now, we see which of the following roots will that the polynomial, P will equal zero.

It seems that -1 can work so by definition, (x+1) is the a factor of the polynomial. So now we use synetheic or long division to cancel out that factor.

So our factored version of the polynomial is

`(x + 1)(3x {}^(3) - 14 {x}^(2) + 13x + 6)`

Now can we continue and factor the right side of the factors.

3 also works so x-3 is a factor as well so

`(3 {x}^(2) - 5x - 2)(x + 1)(x - 3)`

Now factor the quadratic using factoring by grouping

`3 {x}^(2) - 5x - 2 = 3 {x}^(2) - 6x + x - 2 = 3x(x - 2) + 1(x - 2)`

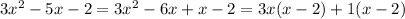
So our factor are

`(3x + 1)(x - 2)`

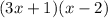
So in conclusion our factors are

`(3x + 1)(x - 2)(x + 1)(x - 3)`

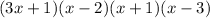
And our x values are -1/3, 2, -1, and 3.