Answer:
Not a parallelogram.
Explanation:
By the midpoint formula, the midpoint of a segment between
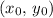 and
and
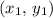 is:
is:
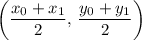 .
.
A quadrilateral is a parallelogram if and only if the midpoints of the two diagonals are the same.
The two diagonals of quadrilateral
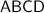 are segment
are segment
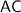 and segment
and segment
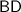 , respectively.
, respectively.
Using the midpoint formula, the midpoint of segment
 (between
(between
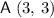 and
and
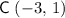 ) would be:
) would be:
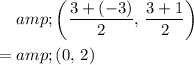 .
.
Likewise, the midpoint of segment
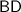 (between
(between
 and
and
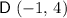 would be
would be
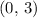 .
.
Thus, quadrilateral
 would not be a parallelogram since the midpoints of its two diagonals are not the same.
would not be a parallelogram since the midpoints of its two diagonals are not the same.