Answer:
Approximately
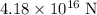 .
.
Step-by-step explanation:
Consider two objects of mass
 and
and
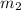 . Let
. Let
 denote the distance between the center of mass of each object. Let
denote the distance between the center of mass of each object. Let
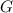 denote the gravitational constant. (
denote the gravitational constant. (
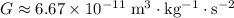 .)
.)
By Newton's Law of Universal Gravitation, the size of gravitational attraction between these two objects would be:
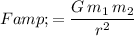 .
.
In this question,
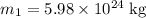 and
and
 are the mass of the two planets. The distance between the two planets is
are the mass of the two planets. The distance between the two planets is
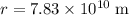 (approximately the same as the distance between the center of mass of planet Earth and the center of mass of Mars.)
(approximately the same as the distance between the center of mass of planet Earth and the center of mass of Mars.)
Apply Newton's Law of Universal Gravitation to find the size of gravitational attraction between the two planets:
 .
.
Since
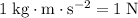 , the size of gravitational attraction between the two planets would be approximately
, the size of gravitational attraction between the two planets would be approximately
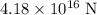 .
.