x is the days that the first team finishes the work alone (x>8)
y --------------------------second-----------------------------------------(y>8)
In a day:
- The first team finishes 1/x (the work)
- The second team finishes 1/y (the work)
- Two teams working together finish 1/8 (the work)
⇒
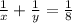 (1)
(1)
If the first team works alone for two days and the second team works alone for 5 days, 5/8 of the total work still remains:
⇒
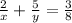 (2)
(2)
(1),(2) ⇒
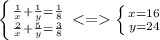
It'll take the first team 16 days and the second team 24 days to finish the work alone
ok done. Thank to me :>