we can always get the common ratio of a geometric sequence by simply dividing the current term by the previous term, in this case for the sake of simplicity let's divide 2/3 by 2, so
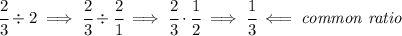
so the sequence more or less looks like
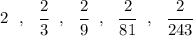
so we'd want the sum of the first 5 terms
