Question

Find the absolute maximum and minimum values of function f on the set D.f(x,y) = e^-x^2-y^2()x^2+2y^2; D is the disk x^2+y^2<=4

Answer 1

You probably mean the function to be

`f(x, y) = e^(-x^2-y^2) (x^2 + 2y^2)`

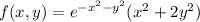
We use the second (partial) derivative test for this.

Compute the first partial derivatives of f :

`(\partial f)/(\partial x) = e^(-x^2-y^2)(2x - 2x(x^2+2y^2)) = e^(-x^2-y^2) (2x - 2x^3 + 4xy^2)`

`(\partial f)/(\partial y) = e^(-x^2-y^2)(4y - 2y(x^2+2y^2)) = e^(-x^2-y^2) (4y-4y^3-2x^2y)`

Find the critical points of f, where both first derivatives vanish. Since
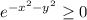`e^(-x^2-y^2)\ge0` for all x and y, we're left with

`2x - 2x^3 - 4xy^2 = 2x (1 - x^2 - 2y^2)= 0`

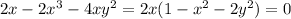
which means either x = 0 or x² + 2y² = 1, and

`4y - 4y^3 - 2x^2y = 2y (2 - 2y^2 - x^2) = 0`

so y = 0 or x² + 2y² = 2.

• If x = 0 and y = 0, then one critical point is (0, 0).

• If x ≠ 0 and y = 0, then x² + 2y² = x² = 1, which means x = ±1. So we have two additional critical points, (-1, 0) and (0, 0).

• If x = 0 and y ≠ 0, then x² + 2y² = 2y² = 2, so y² = 1 and y = ±1, and we get two more critical points at (0, -1) and (0, 1).

All five of these critical points belong to D.

Compute the Hessian matrix for f and check the sign of its determinant at each critical point. Remember what the second partial derivative test concludes:

• If det H(x, y) is negative, then that point is a saddle point

• If det H(x, y) is positive, and ∂²f/∂x² is negative, then that point is a maximum

• If det H(x, y) is positive, and ∂²f/∂x² is positive, then that point is a minimum

The Hessian matrix for f is

`H(x,y) = \begin{bmatrix}(\partial^2f)/(\partial x^2) & (\partial^2f)/(\partial y\partial x) \\ (\partial^2f)/(\partial x\partial y) & (\partial^2f)/(\partial y^2)\end{bmatrix}`

`H(x,y) = \begin{bmatrix}2 - 10 x^2 + 4 x^4 - 4 y^2 + 8 x^2 y^2 & -12 x y + 4 x^3 y + 8 x y^3 \\ -12 x y + 4 x^3 y + 8 x y^3 & 4 - 2 x^2 - 20 y^2 + 4 x^2 y^2 + 8 y^4\end{bmatrix} e^(-x^2-y^2)`

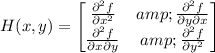
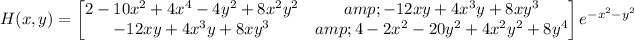
Note that ∂²f/∂x² is the (1, 1) entry. Compute the determinant and evaluate it at each critical point.

`\det H(0,0) = \det\begin{bmatrix}2&0\\0&4\end{bmatrix} = 8 > 0`

`(\partial^2f)/(\partial x^2) (0, 0) = 2 > 0`

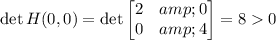
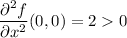
⇒ local minimum at (0, 0) of f(0, 0) = 0

`\det H(-1, 0) = \det\begin{bmatrix}-\frac4e & 0 \\ 0 & \frac2e\end{bmatrix} = -\frac8{e^2} < 0`

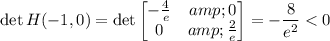
⇒ saddle point (-1, 0)

`\det H(1, 0) = \det\begin{bmatrix}-\frac4e & 0 \\ 0 & \frac2e\end{bmatrix} = -\frac8{e^2} < 0`

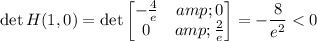
⇒ saddle point at (1, 0)

`\det H(0,-1) = \det\begin{bmatrix}-\frac2e & 0 \\ 0 & -\frac8e\end{bmatrix} = (16)/(e^2) > 0`

`(\partial^2f)/(\partial x^2) (0,-1) = -\frac2e < 0`

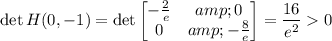
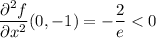
⇒ local maximum at (0, -1) of f(0, -1) = 2/e ≈ 0.736

`\det H(0,1) = \det\begin{bmatrix}-\frac2e & 0 \\ 0 & -\frac8e\end{bmatrix} = (16)/(e^2) > 0`

`(\partial^2f)/(\partial x^2) (0,1) = -\frac2e < 0`

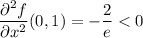
⇒ local maximum at (0, 1) of f(0, 1) = 2/e ≈ 0.736

Check for extrema along the boundary. We can parameterize the boundary by setting

x(t) = 2 cos(t)

y(t) = 2 sin(t)

with 0 ≤ t < 2π. Then f(x, y) = f(x(t), y(t)) reduces to a function of only t, which we call F(t) :

`f(2 \cos(t), 2 \sin(t)) = e^(-4\cos^2(t)-4\sin^2(t)) (4\cos^2(t) + 8 \sin^2(t))`

`\implies F(t) = \frac4{e^4} (1 + \sin^2(t)) = \frac2{e^4} (3 - \cos(2t))`

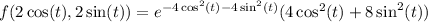
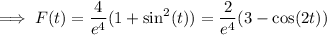
Find the critical points of F on the interval [0, 2π) :

`F'(t) = \frac4{e^4} \sin(2t) = 0`

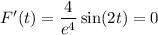
sin(2t) = 0

2t = arcsin(0) + 2nπ or 2t = π - arcsin(0) + 2nπ

(where n is any integer)

2t = 2nπ or 2t = π + 2nπ

t = nπ or t = π/2 + nπ

Over [0, 2π), critical points occur at t = 0, t = π/2, t = π, and t = 3π/2.

Check the sign of the second derivative of F at each critical point. The test in the one-variable case says

• if F''(t) < 0, then that point is a maximum

• if F''(t) > 0, then that point is a minimum

`F''(t) = \frac8{e^4} \cos(2t)`

`F''(0) = \frac8{e^4} > 0`

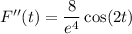
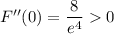
⇒ local minimum when t = 0 of F(0) = 4/e⁴ ≈ 0.0733. This t corresponds to the point (2, 0), since x(0) = 2 and y(0) = 0.

`F''\left(\frac\pi2\right) = -\frac8{e^4} < 0`

⇒ local maximum when t = π/2 of F(π/2) = 8/e⁴ ≈ 0.147, referring to the point (0, 2)

`F''(\pi) = \frac8{e^4} > 0`

⇒ local minimum when t = π of F(π) = 4/e⁴ ≈ 0.0733 at the point (-2, 0)

`F''\left(\frac{3\pi}2\right) = -\frac8{e^4} < 0`

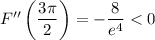
⇒ local maximum when t = 3π/2 of F(3π/2) = 8/e⁴ ≈ 0.147 at (0, -2)

So, the absolute extrema of f(x, y) over D are

• minimum : f(0, 0) = 0

• maximum : f(0, -1) = f(0, 1) = 2/e ≈ 0.736