Question

What is the area of a triangle whose vertices are R(-4, 2). S(1, 2), and T(-5, - 4) ?

Enter your answer in the box.
units2

Answer 1

-15 sq. units

Explanation:

To solve this, we'll use the formula.

Coordinate Geometry formula for a triangle:

`(1)/(2) [(x_1 (y_2 - y_3) + x_2 (y_3 - y_1) + x_3(y_1 - y_2)]`

R(−4, 2), S(1, 2), and T(−5, −4) as the vertices of △RST

`x_1 = - 4, y_1 = 2`

`x_2 = 1, y_2 = 2`

`x_3 = - 5, y_3 = - 4`

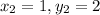
Plugin the values; solve

`(1)/(2) [-4 (2 - (-4)) + 1 (- 4 - 2) + (-5) (2 - 2)]`

`=(1)/(2) [-24 - 6 - 0]`

`= (1)/(2) [-30]`

`= (-30)/(2)`

`= -15`

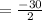
Therefore, the area of the triangle is -15 sq. units.