Answer:
k = -3
Explanation:
The expression evaluates at x=3 to ...
(2·3² +3k -9)/(3² -4·3 +3) = (9+3k)/0
In order for the limit to exist, there must be a "hole" at x=3. That will only be the case when ...
9 +3k = 0
k = -9/3 = -3
The value of k must be -3 for the limit to exist.
__
When k=-3, the expression factors as ...
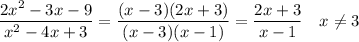
The limit as x→3 is 9/2.