Answer:
Width = 10 inches
Explanation:
Given the perimeter of a rectangle of 68 inches, and a length that is 14 inches longer than its width.
We can establish the following values to help us solve for the width of a rectangle:
Perimeter (P) = 68 inches
Length (L) = 14 + W inches
Width (W) = unknown
Solve for the Width (W)
P = 2(L + W) ⇒ This is the same as P = 2L + 2W, except that 2 is factored out from the right-hand side.
Divide both sides by 2:
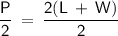
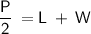
Substitute the value of the Perimeter and the length (L) into the formula:
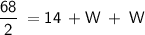
Combine like terms on the right-hand side, and simplify the left-hand side of the equation:

Subtract 14 from both sides:
34 - 14 = 14 - 14 + 2W
20 = 2W
Divide both sides by 2 to solve for the width (W):
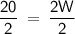
W = 10 inches
Therefore, the width of the rectangle is 10 inches.
Double-check:
Verify whether the derived value for the width is correct:
P = 2L + 2W
68 = 2(14 + 10) + 2(10)
68 = 2(34) + 20
68 = 48 + 20
68 = 68 (True statement).
Thus, the length of the rectangle is 34 inches, and the width is 10 inches.