Answer:
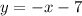 .
.
Explanation:
Slope of the given line segment:
 .
.
The slope of any line perpendicular to this line segment would be:
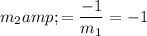 .
.
Midpoint of the given line segment:
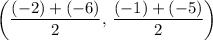 .
.
Simplifies to get:
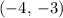 .
.
Find the equation of the perpendicular bisector in point-slope form and simplify.
 .
.
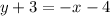 .
.
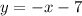 .
.