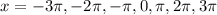Answer:
7 inflection points
Explanation:
The given function
 has a midline of y=2 where each point of the function that intersects the line is an inflection point. Inflection points are where the concavity changes, defined by when the second derivative is equal to 0 or undefined.
has a midline of y=2 where each point of the function that intersects the line is an inflection point. Inflection points are where the concavity changes, defined by when the second derivative is equal to 0 or undefined.
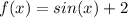

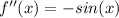
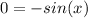
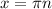 for any integer
for any integer

From
![[-10,10]](https://img.qammunity.org/2022/formulas/mathematics/high-school/780lvedxgbv3379ewbhdcdtid75vx3c7sg.png) , there are 7 inflection points, which are
, there are 7 inflection points, which are