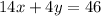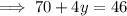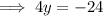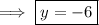If the given equations are indeed

we can solve by substitution. Solve the second equation for x :


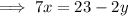
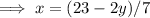
Substitute this into the first equation and solve for y :
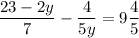
On the right side, write the mixed number as an improper fraction:
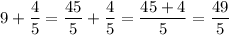
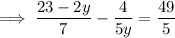
Multiply both sides of this equation by 35y (the LCM of the denominator of all three fractions)
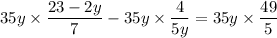
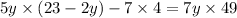
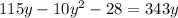
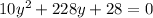
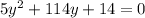
To solve the quadratic, I'll complete the square :
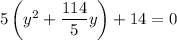


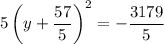
This system has no real solutions since the square of any real number must be positive.
If we allow complex numbers, we can continue solving to end up with two complex solutions for y,
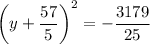
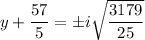
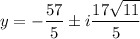
and we can go on to solve for x.
Hence my comment; I suspect you meant to write the system
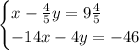
because its solution is far simpler. Multiplying through the first equation by 5 gives
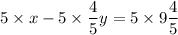

(since we know 9 + 4/5 = 49/5)
Meanwhile, multiplying through the second equation by -1 gives

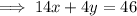
So if we combine the two equations, we can eliminate y and solve for x :
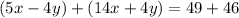
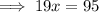

and solving for y gives