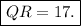Answer:
A. 17
Explanation:
Let X be the intersection of lines QR and NP.
By Power of a Point, we have
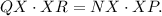
(This can be proven with similar triangles by connecting QN and PR and using proportions with similar triangles
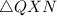 and
and
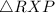 .)
.)
Plugging the values we know into
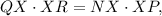 we have
we have
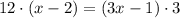 .
.
Dividing both sides by 3 gives
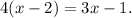
Distributing the left hand side gives
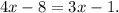
Subtracting 3x from both sides, we have

Finally, adding 8 to both sides, we have

The question asks to find QR. (I'm assuming this is what you meant in the question.) With the lengths given, we know

Therefore, plugging x in gives us