Question

Bonus: (It's not that hard, you just have to pay attention to units.) The Saturn V rocket first stage

engines produced 7.5 million pounds of thrust at liftoff by burning and exhausting 15 tons of fuel
each second. Determine the velocity of the exhaust gasses. (Be careful with units!) (1 pound = 4.45
Newtons) (1 ton = 2000 pounds) (1kg = 2.2 lbs)

Answer 1

`v = 2.45×10^3\:\text{m/s}`

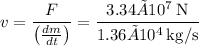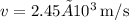
Step-by-step explanation:

Newton's 2nd Law can be expressed in terms of the object's momentum, in this case the expelled exhaust gases, as

`F = \frac{d{p}}{d{t}}` (1)

Assuming that the velocity remains constant then

`F = (d)/(dt)(mv) = v(dm)/(dt)`

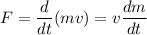
Solving for
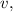`v,` we get

`v = (F)/(\left((dm)/(dt)\right))\;\;\;\;\;\;\;(2)`

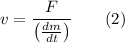
Before we plug in the given values, we need to convert them first to their appropriate units:

The thrust F is

`F = 7.5×10^6\:\text{lbs}×\frac{4.45\:\text{N}}{1\:\text{lb}} = 3.34×10^7\:\text{N}`

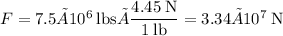
The exhaust rate dm/dt is

`(dm)/(dt) = 15(T)/(s)×\frac{2000\:\text{lbs}}{1\:\text{T}}×\frac{1\:\text{kg}}{2.2\:\text{lbs}}`

`\;\;\;\;\;= 1.36×10^4\:\text{kg/s}`

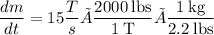
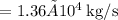
Therefore, the velocity at which the exhaust gases exit the engines is

`v = (F)/(\left((dm)/(dt)\right)) = \frac{3.34×10^7\:\text{N}}{1.36×10^4\:\text{kg/s}}`

`\;\;\;= 2.45×10^3\:\text{m/s}`