Answer:
The balance is $410.06
Explanation:
Given:
P = Principal amount: $1,100
r = Interest rate: 8 % or 0.08
n = compounded quarterly: 4
t = years: 4
This is the formula:
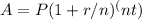
Insert the values
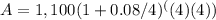
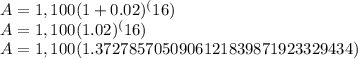
A = 1510.0642755996734023859115662377 or $1,510.06
Now subtract 1,510.06 to 1,100 to find the balance.
1,510.06 - 1,100 = $410.06