Answer:
240
Explanation:
We need to find the coeffeicent of the binomial expansion of
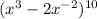
Note that
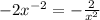
The binomial theorem states that
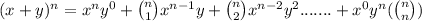
Using this, we let expand our series
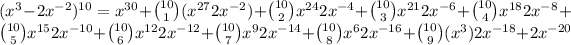
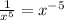
So what term in the series eqaul x^-5.
That term is the 10 choose 7 term.
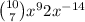
Because
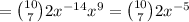
So we need to compute 10 choose 7.
That equals
10!/3!(7!)= 10×9×8/6= 720/6=120.
So we get
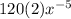
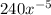
So the coeffceint u
is 240