Question

How can i prove this property to be true for all values of n, using mathematical induction.

ps: spam/wrong answers will be reported and blocked.​

Answer 1

Proof -

So, in the first part we'll verify by taking n = 1.

`\implies \: 1 = {1}^(2) = (1(1 + 1)(2 + 1))/(6)`

`\implies{ (1(2)(3))/(6) }`

`\implies{ 1}`

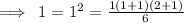
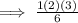
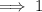
Therefore, it is true for the first part.

In the second part we will assume that,

`\: { {1}^(2) + {2}^(2) + {3}^(2) + ..... + {k}^(2) = (k(k + 1)(2k + 1))/(6) }`

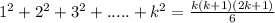
and we will prove that,

`\sf{ \: { {1}^(2) + {2}^(2) + {3}^(2) + ..... + {k}^(2) + (k + 1)^(2) = \frac{(k + 1)(k + 1 + 1) \{2(k + 1) + 1\}}{6}}}`

`\: {{1}^(2) + {2}^(2) + {3}^(2) + ..... + {k}^(2) + (k + 1)^(2) = ((k + 1)(k + 2) (2k + 3))/(6)}`

`{1}^(2) + {2}^(2) + {3}^(2) + ..... + {k}^(2) + (k + 1)^(2) = (k (k + 1) (2k + 1) )/(6) + ((k + 1) ^(2) )/(6)`

`{1}^(2) + {2}^(2) + {3}^(2) + ..... + {k}^(2) + (k + 1)^(2) = (k(k+1)(2k+1)+6(k+1)^ 2 )/(6)`

`{1}^(2) + {2}^(2) + {3}^(2) + ..... + {k}^(2) + (k + 1)^(2) = \frac{(k+1)\{k(2k+1)+6(k+1)\} }{6}`

`{1}^(2) + {2}^(2) + {3}^(2) + ..... + {k}^(2) + (k + 1)^(2) = ((k+1)(2k^2 +k+6k+6) )/(6)`

`{1}^(2) + {2}^(2) + {3}^(2) + ..... + {k}^(2) + (k + 1)^(2) = ((k+1)(2k^2+7k+6) )/(6)`

`{1}^(2) + {2}^(2) + {3}^(2) + ..... + {k}^(2) + (k + 1)^(2) = ((k+1)(k+2)(2k+3) )/(6)`

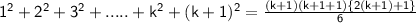
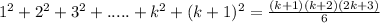
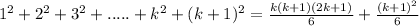
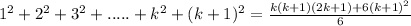
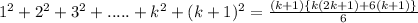
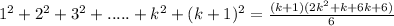
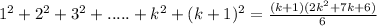
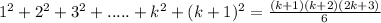
Henceforth, by using the principle of mathematical induction 1²+2² +3²+....+n² = n(n+1)(2n+1)/ 6 for all positive integers n.

_______________________________

Please scroll left - right to view the full solution.