Question

The length of a planet's orbit around a star is approximately 22,200,000 km. It takes the planet about 1230 Earth days to complete a full orbit. What is the planet's average speed in kmh-1 to 3sf?​

Answer 1

Approximately
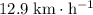`12.9\; \rm km \cdot h^(-1)`, assuming that this orbit is circular.

Explanation:

The question is asking for a tangential velocity with the unit
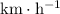`\rm km \cdot h^(-1)`. The unit of the given distance is already in
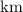`\rm km` as required. Convert the unit of the orbital period to hours:

`\begin{aligned}T &= 1230\; \text{day} * \frac{24\; \rm h}{1\; \text{day}}. = 29520\; \rm h\end{aligned}`.

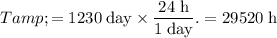Calculate the angular velocity
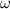`\omega` of this planet from its orbital period:

`\begin{aligned}\omega &= (2\, \pi)/(T) \\ &= (2\, \pi)/(29520\; \rm h) \approx 2.1285 * 10^(-4)\; \rm h^(-1)\end{aligned}`.

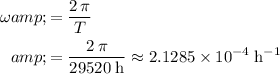Given the radius
`r` of the orbit of this planet, the tangential velocity
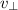`v_(\perp)` of this planet would be:

`\begin{aligned}v_(\perp) &= \omega\, r \\ &\approx 2.1285 * 10^(-4)\; \rm h^(-1) * 2.22* 10^(7)\; \rm km \\ &\approx 4.73 * 10^(3)\; \rm km \cdot h^(-1)\end{aligned}`.

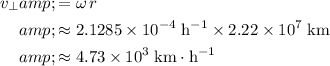If the orbit of this planet is circular, the velocity of the planet would be equal to its tangential velocity:
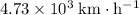`4.73* 10^(3)\; \rm km \cdot h^(-1)`.