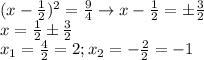Question

X^2-x-2=0 as a complete square

Answer 1

`x_1=2; x_2=-1`

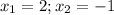
Explanation:

The square term is
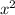`x^2` so we expect the complete square to be of the form
`(x-a) ^2=x^2+2ax+a^2`.

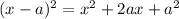Let's compare the first degree terms now: we have
`2ax` on one side and
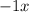`-1x` on the other. That would make
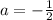`a=- \frac12`. At this point we have still the second squared term, so we add and subtract
`\frac14 = (\frac12)^2`

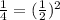
Our equation becomes:

`x^2-x+\frac14 -\frac14-2 =0\\(x-\frac12)^2-\frac94=0`

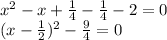
(the
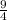`\frac94` term comes from rewriting
`2= \frac84` and adding the terms out of the bracket).

At this point it's just solving the equation:

`(x-\frac12)^2 = \frac94 \rightarrow x-\frac12=\pm\frac32\\x=\frac12\pm\frac32\\x_1=\frac42 = 2; x_2=\fra-\frac22=-1`