Question

Please help! Steps if possible: If n=31, ¯x (x-bar)=41, and s=12, construct a confidence interval at a 90% confidence level. Assume the data came from a normally distributed population.

Give your answers to one decimal place.
decimal place.

________ < μ < _______

Answer 1

Answer:
`\boldsymbol{37.5} < \mu < \boldsymbol{44.5}`

===========================================================

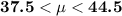
Step-by-step explanation:

At a 90% confidence level, the z critical value is roughly z = 1.645. Use a reference table or a calculator to determine this. Despite not knowing what sigma is, we can use a z interval here because n > 30. If the sample size n was smaller than 30, then we'd have to use a T distribution instead.

We'll plug that z value, along with the other given values, into the formula for the lower boundary L of the confidence interval.

`L = \text{lower boundary}\\\\L = \overline{x} - z*(s)/(√(n))\\\\L = 41 - 1.645*(12)/(√(31))\\\\L = 41 - 3.545\\\\L = 37.455\\\\L = 37.5\\\\`

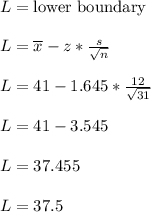
This value is approximate.

Do the same for the upper boundary as well

`U = \text{upper boundary}\\\\U = \overline{x} + z*(s)/(√(n))\\\\U = 41 + 1.645*(12)/(√(31))\\\\U = 41 + 3.545\\\\U = 44.545\\\\U = 44.5\\\\`

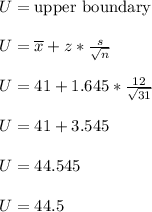
This value is also approximate.

We have 90% confidence that the population mean
`\mu` (greek letter mu) is somewhere between L = 37.5 and U = 44.5

Therefore, we would write the 90% confidence interval as
`\boldsymbol{37.5} < \mu < \boldsymbol{44.5}`

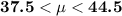
This is the same as writing the confidence interval in the form
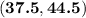`(\boldsymbol{37.5} , \boldsymbol{44.5})`. Both forms are two different ways to say the same thing. The first form being
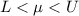`L < \mu < U` while the second form is
`(L,U)`.

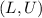Side note: The value 3.545 calculated earlier is the approximate margin of error.