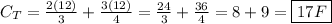Hi there!
Recall the following.
Capacitors in series:
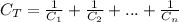
Capacitors in parallel:

Begin by solving for the resulting capacitance of both paths.
Path on the left:
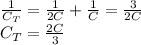
Path on the right:
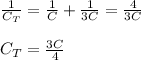
Now, since we ADD capacitors in parallel, we can add the resulting capacitances together:
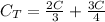
Substitute in 12 F for C and solve.